Illusion géométrique

Comme vous savez, j’aime bien les illusions, et surtout le challenge d’essayer de savoir comment elles marchent. En faisant ma revue quotidienne de blogs je suis tombé sur un puzzle géométrique qui m’a laissé perplexe pendant un petit moment, jusqu’à que j’ai réussi à trouver l’explication. Je ne pouvais donc résister la tentation de vous la présenter ici.
Regardez donc l’image suivante :
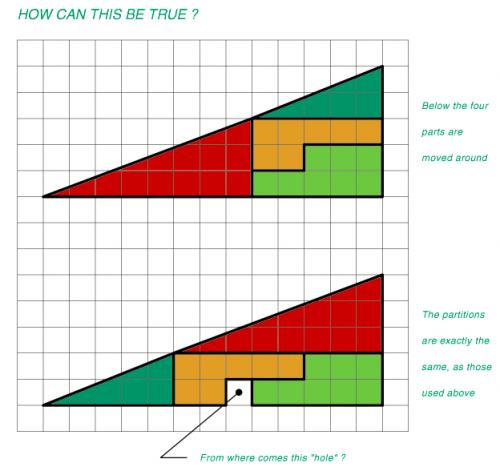
Il semble impossible, mais les pièces sont les mêmes en haut et en bas. Alors, il vient d’où ce trou libre dans l’image inférieur ?
J’étais persuadé qu’il s’agissait d’un trompe-l’œil intelligent, mais je n’arrivais pas à trouver la faille. Il m’a fallu donc tirer de la trigonométrie et appeler au bon vieux Pytagore pour trouvé la réponse. Mais je ne dis plus, la réponse dans les commentaires…
Trouvé via Maikelnai.
Tags: Illusion
02-10-2007 à 13:01
les trois points qui sont l’hypothénuse (les deux sommets de l’hypothénuse du triangle rouge et l’autre sommet du triangle bleu ) ne sont pas alignés !
me trompes-je ?
02-10-2007 à 14:00
Tu ne te trompes pas, non 🙂
Rappelons nous de ces leçons de trigonométrie, et trouvons la pente de ces deux triangles. Pour un triangle rectangle, a = b tan(A).
Pour le triangle vert, 2 = 5 tan(A), donc A = atan(2/5) = 21.80°
Pour le triangle rouge, 3 = 8 tan(A), donc A = atan(3/8) = 20.55°
La première des figures a donc une pseudo-hypoténuse convexe, avec le triangle rouge en bas et le vert en haut. La deuxième figure a une pseudo-hypoténuse concave. Et c’est pour ça que la surface de la figure 2 est plus grande que celle de la figure 1.
Je ne sais pas si j’arrive à l’expliquer, sinon je ferai un dessin avec les deux pseudo-hypoténuses et la vraie hypoténuse.
10-10-2007 à 14:57
Dans le même style il y a celui-ci :
familycats.canalblog.com/…